A statistical model is a theoretical distribution. It aims to describe a variable from a population. Observations from the population (i.e. the sample) are used to find plausible values for the parameters of the statistical model.

Statistical models are used to:

• Infer properties of a population
• Test hypotheses about a population

Below are a couple of videos giving introductory examples of statistical modelling.

We use the human height data (HEIGHT.CSV) to illustrate the use of a statistical model to infer a property (the average) of a population.

We will infer two numbers:

• an estimate of the average height of women
• an estimate of the uncertainty in this estimated average

Code to simulate one data sample from the statistical model (a normal distribution):

		  # Sample's mean and standard deviation
		  sample_mean = 1.63201
		  sample_sd = 0.063306

		  # Number of observations in the sample
		  n_obs = 1364

		  # Simulate one sample from a normal distribution
		  # with the same number of observations as the sample
		  sim = rnorm(n_obs, mean=sample_mean, sd=sample_sd)
	      

Try running this code in R and calculating the mean of the simulated sample (variable sim).

The distribution of means from 10,000 simulated samples is: The standard deviation of this distribution is one measure of uncertainty in the mean, called the standard error of the mean.
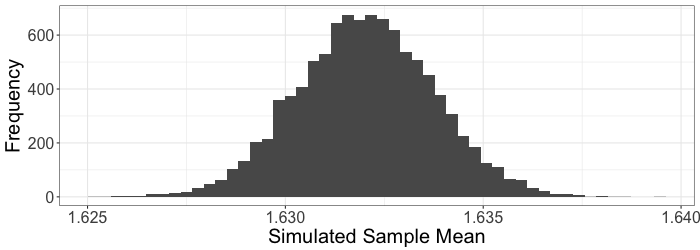
The standard deviation from the histogram above is 0.0017 m.

Our final answer is:

The average height of women aged 20-30 years in the USA is 1.632 m (s.e. = 0.002 m).

Instead of simulating from the statistical model, statistical theory can be used to obtain the uncertainty in the estimated population mean.

Use $\sigma=$0.063306 m and $n=$1364 observations, to see how this theory compares to our simulated result.

We are going to use the dice example to illustrate the idea of using statistical models to test a hypothesis.

The two possible answers to this question can be written as hypotheses:

Hypothesis (H₁): The dice is biased.

Null-Hypothesis (H₀): The dice is unbiased.

I have a dice that I have rolled 20 times, giving these results:

This is a sample of 20 observations from the population.

In this case, the population is an infinite number of rolls of this dice (we will never have complete information about this population).

Code to input observed data from 20 dice rolls:

		  # The observed data from 20 dice rolls
		  dice_data = c(5, 6, 1, 3, 2, 3, 1, 4, 3, 3, 6, 3, 1, 1, 2, 1, 6, 4, 5, 1)
	      

Code to simulate 20 dice rolls from the H₀ model:

		  # Define the categorical distribution for the null, H0 model
		  outcomes = c(1, 2, 3, 4, 5, 6)  # All possible outcomes from a dice
		  probability_H0 = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6) # Outcome probabilities

		  # Create one simulation of 20 dice rolls using the null-hypothesis model
		  sample(outcomes, size=20, prob=probability_H0, replace=T) 
	      

Code to simulate 20 dice rolls from the H₁ model:

		  # Define the categorical distribution for the H1 model
		  outcomes = c(1,2,3,4,5,6)  # All possible outcomes from a dice
		  probability_H1 = c(6/20, 2/20, 5/20, 2/20, 2/20, 3/20) # Outcome probabilities

		  # Create one simulation of 20 dice rolls using the null-hypothesis model
		  sample(outcomes, size=20, prob=probability_H1, replace=T) 
	      

The bias from 20 dice rolls can be quantified by calculating a statistic. $$\text{Bias} = \sum_{i=1}^6 (p_i - 1/6)^2$$ where $p_i$ is the relative frequency of the i^th outcome. If the number one appeared six times in 20 rolls, $p_i=6/20$.

An unbiased dice has $\text{Bias}=0$
A biased dice that always rolled a one has $\text{Bias}=5/6$.

Our 20 observations give a bias of 0.0383.

We will test for bias in our dice using this test statistic

Using the null-model to simulate 10000 sets of data, each containing 20 dice rolls, we can calculate the distribution of bias from an unbiased dice.

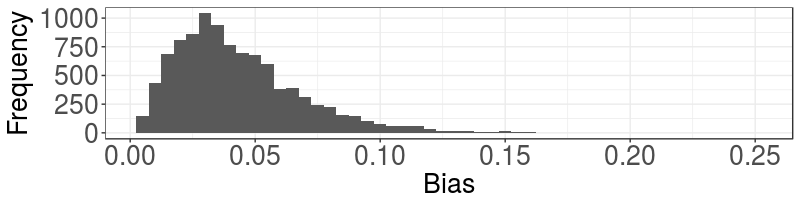
From this distribution we can calculate that 51% of the simulated data had a bias at least as large as the observed bias of 0.0383.